Filtro Digital FIR Passa-faixa com Implementação em MatLab
Questão: Usando a função fir1 do Matlab, projete um filtro FIR passa-faixa de fase linear com as seguintes especificações: frequências limites da faixa de rejeição de $0,6\pi$ e $0,8\pi$, da faixa de passagem $0,65\pi$ e $0,75\pi$, atenuação máxima na faixa de passagem de 0,2 dB e atenuação mínima na faixa de rejeição de 42 dB. Utilize as janelas de Hamming, Hann, Blackman e Kaiser, e mostre a resposta em magnitude de cada um dos filtros obtidos. Comente os resultados.
Resposta: Conteúdo da resposta.
Código em MatLab para filtro FIR passa-faixa com janelamento
Hamming, Hann, Blackman e Kaiser
%% ====== Codigo - Filtro FIR (Janelas) ====== %%
% %
% Aluno: Cleber Gobira %
% Disciplina: Processamento Digital de Sinais %
% %
%% ====== Codigo - Filtro FIR (Janelas) ====== %%
FxaR = [0.6 0.8]; %Faixa de Rejeicao
FxaP = [0.65 0.75]; %Faixa de Passagem em radianos
wc = FxaP; %Banda passante
fsamp = 1000; %frequencia de amostragem
%Em (Hz). Multiplicado por 1000 por coveniencia
fcuts = [0.3 0.325 0.375 0.4]*1000
mags = [0 1 0]; %magnitude
d1 = 10^(-0.05*42) %Ondulacao da banda de corte
d2 = (10^(0.05*0.2)-1)/(10^(0.05*0.2)+1) %ondulacao da banda de passagem
devs = [d1 d2 d1]; %Definicao do desvio
[n,Wn,beta,ftype] = kaiserord(fcuts,mags,devs,fsamp); %para obter a ordem
JanKaiser = fir1(n,Wn,ftype,kaiser(n+1,beta));
%% Janela de Hanning
h1 = hann(n+1);
JanHann = fir1(n,Wn,h1);
%% janela HAMMING
h2 = hamming(n+1);
JanHamm = fir1(n,Wn,h2);
%% janela blackman
b1 = blackman(n+1);
JanBlac = fir1(n,Wn,b1);
%% Plotando
plotall = fvtool(JanHamm,1,JanHann,1,JanBlac,1,JanKaiser,1);
legend(plotall,'Hamming','Hanning','Blackman','Kaiser');
title('Resposta em Magnitude (Janela Hamming, Hanning, Blackman, kaiser)');
Clique na imagem para melhor visualização
 |
| Figura 1 – Filtro passa-faixa FIR com janelamento Kaiser com fase linear. |
 |
| Figura 2 – Fase linear do filtro passa-faixa FIR com janelamento Kaiser. |
 |
| Figura 3 – Filtro passa-faixa FIR com janelamento Hamming, Hanning, Blackman e Kaiser, com fase linear. |
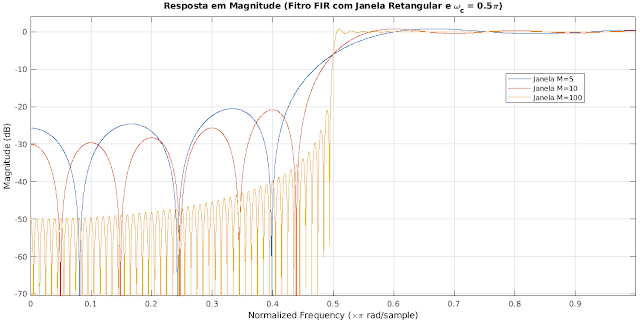
Para reduzir o efeito do fenômeno de Gibbs, deve-se usar janelas com truncamento menos abrupto. Em alguns casos é necessário a utilização de janelas mais sofisticadas, o uso de algumas delas podem ser observadas nas figuras 1 e 3, que são algumas das mais usuais. São poucas as diferenças entre as janelas Hamming, Hanning e Blackman, e essas diferenças estão voltadas a redução do fenômeno de Gibbs.
É importante salientar que entre as janelas citadas a janela de Kaiser é a única onde é possível especificar os parâmetros do filtro. Além disso elá é considerada ótima porque provê um lóbulo principal largo para a dada atenuação da banda de corte, o que implica a mais brusca banda de transição. Na figura 3, pode-se comparar a implementação com diferentes tipos de janela e constatar que quando usado a janela de kaiser é possível conseguir com muito mais precisão o requisitos de projeto do filtro FIR.
REFERÊNCIAS:
OPPENHEIM, Alan V.; SCHAFER, Ronald W. Discrete-time signal processing. Pearson Education, 3rd Edition, 2016.
Tags: filtro digital matlab filtros digitais gibbs janela janelas hamming hanning blackman fir kaiser fase linear janelamento passa-faixa passa faixa alta baixa fir1