Filtro Digital FIR Passa-altas com Implementação em Matlab
Questão: Um filtro discreto ideal passa-altas com fase linear tem a seguinte resposta ao impulso:$$\Large{
h_{HP}[n]=\begin{cases}
1 - \dfrac{\omega_c}{\pi}, & para~n = 0\\
-\dfrac{sen(\omega_c n)}{\pi n}, & para~n \neq 0
\end{cases}}
$$
onde $\omega_c$ é a frequência de corte discreta do filtro. Usando Matlab, mostre a resposta em magnitude de um filtro passa-altas FIR obtido truncando-se a resposta do filtro ideal acima, de comprimento $N = 2M + 1$ (ou seja, $ -M \leqslant n \leqslant M$ ). Obtenha o resultado usando os valores $M = 5$ e $M = 10$. Comente os resultados obtidos.
(A resposta apresentada aqui, pode não estar 100% correta, mas certamente pode ser proveitosa para alguns)
Código em MatLab para $M = 5,~$ $M = 10,~$ $~M = 100~$ e $\omega_{c} = 0.5\pi $:%% == Codigo - Filtro FIR Janela retangular == %%
% Aluno: Cleber Gobira %
% Disciplina: Processamento Digital de Sinais %
%% =========================================== %%
M = 5; % Tamanho da janela
wc = 0.5*pi;
n = 1:M
h0 = 1 - (wc)/pi
haux = (-1./(n.*pi)).*sin(wc.*n) %Impulse Response h[n] p/ Filtro P. Alta
h1 = [fliplr(haux) h0 haux] %Vetor com os coeficientes do filtro
M1 = 10; % Tamanho da janela
n = 1:M1
h0 = 1 - (wc)/pi
haux = (-1./(n.*pi)).*sin(wc.*n) %Impulse Response h[n] p/ Filtro P. Alta
h2 = [fliplr(haux) h0 haux] %Vetor com os coeficientes do filtro
M2 = 100; % Tamanho da janela
n = 1:M2
h0 = 1 - (wc)/pi
haux = (-1./(n.*pi)).*sin(wc.*n)%Impulse Response h[n] p/ Filtro P. Alta
h3 = [fliplr(haux) h0 haux] %Vetor, coeficientes do filtro, fliplr invert vetor
plotall = fvtool(h1,1,h2,1,h3,1);
legend(plotall,'Janela M=5','Janela M=10','Janela M=100')
title('Resposta em Magnitude (Fitro FIR, Janela Retangular, \omega_{c}=0.5\pi)');
Clique na imagem para melhor visualização.
 |
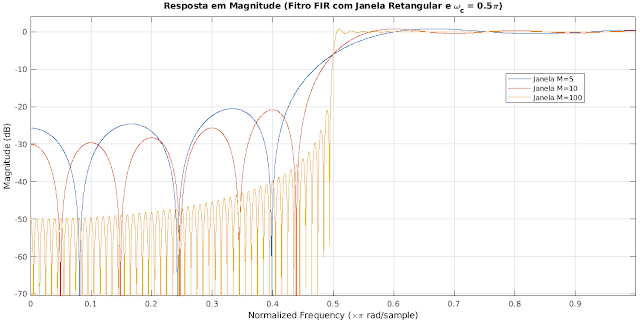
| Figura 1 - Filtro passa-baixas FIR com janelamento retangular para M = 5, 10 e 100. |
Como a janela $w[n]$ tem comprimento finito igual a M, sua resposta em frequência é uma sinc. A região de pico central (lóbulo principal) tem largura proporcional a 1/M e os lóbulos adjacentes com pesos menores. A convolução entre a janela e o filtro ideal gera uma versão da resposta ideal, mas com algumas distorções (ondulações).
A largura da banda de transição é proporcional a 1/M. Os lóbulos laterais produzem ondulações que têm forma similar tanto na banda de passagem quanto na banda de rejeição. Devido a isso pode-se observar ondulações nas extremidades da faixa de passagem, chamado de fenômeno de Gibbs, que surgem devido à descontinuidade imposta pela janela da sequência $h[n]$, ou seja, o corte abrupto da janela retangular.
O aumento de M produz lóbulos com largura menor e mesma área, ou seja, ondulação mais rápida, mas com a mesma amplitude. Isso fica claro quando observamos a Figura 1, onde mostra que a medida que se aumenta M os lóbolos se estreitam e assim temos mais ondulações. Portanto quando se usa M menor temos menos ondulação na banda de passagem, porém o lóbulo principal fica mais largo, aumentando assim a banda de transição e perdendo seletividade. Neste caso deve-se projetar M de forma a obter um equilíbrio para o objetivo almejado. O janelamento retangular não é a melhor forma de se obter um filtro FIR, devido ao corte abrupto.
Veja também: Filtros Digitais - Filtro FIR Passa-faixa - Janelamento de Hamming, Hann, Blackman e Kaiser em Matlab.
REFERÊNCIAS:
OPPENHEIM, Alan V.; SCHAFER, Ronald W. Discrete-time signal processing. Pearson Education, 3rd Edition, 2016.